A Comparison of Five Estimation Methods
The contour plot in figure 5 is generated by computer software using an internal interpolation method to estimate gpc values. The software has been found to be inconsistent. For example, if you look at the value in the small circle (2.0), you'll notice that the 2.0 contour line does not include this cup, as it should.
These plots help determine line lengths, usually expressed in feet, at different coverage levels within a ground pattern. In an attempt to improve the contour plots and line length estimates, five interpolation methods were examined and compared. The five methods are polygonal declustering, triangulation, inverse distance weighting, local sample mean, and ordinary kriging (Kaluzny and others 1998). These five methods are point estimators that use distance (and other factors) as a basis for estimation. When estimating points in space, it is generally assumed that points closer together are more alike than points farther apart. Under this assumption, more weight is given to points that are closer together.
Cross validation was used to assess the performance of each of the five methods. Cross validation is a technique where the observed sample data are used to make estimations and the estimates are compared to the observed sample data. For example, 543 sample values make up the observed data set in drop 201. One observed value is removed and the remaining 542 values are used to predict a gpc value for the removed value. Once that calculation is complete, the observed value is put back and another observed value is removed. The remaining 542 values are used to predict gpc for the removed value. This process is repeated until a prediction has been made at each of the 543 locations. The result is 543 original observed sample values and 543 estimated values at the same locations. The estimates are compared to the observed data to determine how well the estimation method performed.
Table 1 shows the cross-validation results for drop 201. Triangulation depends on three points to make a prediction, so it cannot predict points in the corners of the grid. For this reason, cross validation produces fewer predicted values when triangulation is used. The observed gpc values at those sites were removed for comparison purposes.
| Summary statistics for five point-estimation methods for drop 201 (gpc) | |||||||
|---|---|---|---|---|---|---|---|
| TRUE | Triangulation | TRUE | Ordinary kriging | Polygonal declustering | Inverse distance squared | Local sample mean | |
| Mean | 0.76 | 0.76 | 0.75 | 0.75 | 0.76 | 0.79 | 0.89 |
| Standard deviation | 1.21 | 1.12 | 1.20 | 1.05 | 1.20 | 0.59 | 0.30 |
| Minimum | 0.00 | 0.00 | 0.00 | -0.40 | 0.00 | 0.07 | 0.28 |
| 1st quartile | 0.01 | 0.02 | 0.01 | 0.04 | 0.02 | 0.34 | 0.69 |
| Median | 0.23 | 0.29 | 0.22 | 0.29 | 0.23 | 0.59 | 0.93 |
| 3rd quartile | 1.15 | 1.12 | 1.13 | 1.19 | 1.13 | 1.13 | 1.06 |
| Maximum | 14.66 | 9.98 | 14.66 | 6.74 | 14.66 | 3.60 | 1.66 |
| Correlation | 0.92 | 0.84 | 0.70 | 0.80 | 0.09 | ||
| n | 537 | 537 | 543 | 543 | 543 | 543 | 543 |
| Summary statistics for error distribution of point-estimation methods (gpc) | |||||
|---|---|---|---|---|---|
| Triangulation | Ordinary kriging | Polygonal declustering | Inverse distance squared | Local sample mean | |
| Mean | -0.00016 | 0.00127 | -0.00558 | -0.034233 | -0.13836 |
| Standard deviation | 0.465 | 0.660 | 0.924 | 0.813 | 1.213 |
| Minimum | -6.070 | -3.034 | -12.140 | -1.475 | -1.614 |
| 1st quartile | -0.015 | -0.126 | -0.045 | -0.387 | -0.927 |
| Median | 0.000 | -0.017 | 0.000 | -0.186 | -0.452 |
| 3rd quartile | 0.080 | 0.102 | 0.160 | 0.080 | 0.357 |
| Maximum | 4.685 | 10.550 | 9.370 | 12.327 | 13.693 |
| MAE | 0.191 | 0.267 | 0.377 | 0.433 | 0.865 |
| MSE | 0.215 | 0.435 | 0.852 | 0.661 | 1.489 |
| n | 537 | 543 | 543 | 543 | 543 |
The method that produces estimates that most closely resemble observed data is considered the best. Both triangulation and ordinary kriging have means identical to the observed data. The local sample mean has the least amount of variability, indicating that it smooths the most. Smoothing is similar to averaging. It provides an overview of underlying trends, but information can be lost with excessive smoothing. Examining the five-number summary (minimum, first quartile, median, third quartile, and maximum) gives an idea of the spread of the predicted values compared with the observed. Overall, the predictions have less spread than the true values except when polygonal declustering is used. All of the prediction methods, except for polygonal declustering, smooth data to some extent. Of the other four methods, local sample mean smooths the most and triangulation smooths the least. Triangulation has the highest correlation coefficient, while local sample mean has the lowest.
The second part of table 1 displays the summary statistics for the error of the five-point estimators. Error (also called residual) is the difference between the predicted value and the true value. The table of summary statistics for error shows extreme residuals as well as the mean absolute error (MAE) and the mean squared error (MSE). The MSE is the mean of the squared residuals. Residuals are squared to eliminate negative numbers. The MAE is the mean of the absolute value of the residuals. Taking the absolute value removes negative signs to provide a more meaningful statistic. A good prediction method would produce low MAE and MSE values (Isaaks and Srivastava 1989).
The residual means closest to zero were produced by triangulation and ordinary kriging. Triangulation produces the lowest MAE and MSE with ordinary kriging producing the second lowest.
After examining three drops (tables 1, 2, and 3), triangulation appears to perform the best as a prediction method, with ordinary kriging performing second best. These findings indicate that either triangulation or ordinary kriging could be used as a reliable estimator for drop-test data.
| Summary statistics for five point-estimation methods for drop 203 (gpc) | |||||||
|---|---|---|---|---|---|---|---|
| TRUE | Triangulation | TRUE | Ordinary kriging | Polygonal declustering | Inverse distance squared | Local sample mean | |
| Mean | 0.74 | 0.74 | 0.73 | 0.73 | 0.73 | 0.76 | 0.79 |
| Standard deviation | 1.24 | 1.13 | 1.24 | 1.07 | 1.24 | 0.53 | 0.14 |
| Minimum | 0.00 | 0.00 | 0.00 | -0.52 | 0.00 | 0.10 | 0.39 |
| 1st quartile | 0.01 | 0.01 | 0.00 | 0.02 | 0.01 | 0.36 | 0.70 |
| Median | 0.05 | 0.11 | 0.05 | 0.19 | 0.05 | 0.56 | 0.84 |
| 3rd quartile | 1.06 | 1.14 | 1.04 | 1.20 | 1.04 | 1.08 | 0.89 |
| Maximum | 11.80 | 7.78 | 11.80 | 5.71 | 11.80 | 2.65 | 0.99 |
| Correlation | 0.91 | 0.83 | 0.66 | 0.78 | 0.03 | ||
| n | 538 | 538 | 544 | 544 | 544 | 544 | 544 |
| Summary statistics for error distribution of point-estimation methods (gpc) | |||||
|---|---|---|---|---|---|
| Triangulation | Ordinary kriging | Polygonal declustering | Inverse distance squared | Local sample mean | |
| Mean | -0.00002 | 0.00365 | -0.00072 | -0.03169 | -0.06105 |
| Standard deviation | 0.512 | 0.695 | 1.018 | 0.884 | 1.240 |
| Minimum | -5.040 | -2.439 | -10.090 | -1.216 | -0.992 |
| 1st quartile | -0.006 | -0.155 | -0.020 | -0.443 | -0.852 |
| Median | 0.000 | -0.014 | 0.000 | -0.271 | -0.595 |
| 3rd quartile | 0.070 | 0.140 | 0.140 | -0.022 | 0.289 |
| Maximum | 4.025 | 8.160 | 8.050 | 10.083 | 11.089 |
| MAE | 0.225 | 0.345 | 0.445 | 0.537 | 0.898 |
| MSE | 0.262 | 0.482 | 1.035 | 0.780 | 1.539 |
| n | 538 | 544 | 544 | 544 | 544 |
| Summary statistics for five point-estimation methods for drop 205 (gpc) | |||||||
|---|---|---|---|---|---|---|---|
| TRUE | Triangulation | TRUE | Ordinary kriging | Polygonal declustering | Inverse distance squared | Local sample mean | |
| Mean | 0.78 | 0.78 | 0.77 | 0.77 | 0.80 | 0.81 | 0.81 |
| Standard deviation | 1.47 | 1.38 | 1.47 | 1.26 | 1.46 | 0.81 | 0.35 |
| Minimum | 0.00 | 0.00 | 0.00 | -0.64 | 0.00 | 0.01 | 0.08 |
| 1st quartile | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.21 | 0.58 |
| Median | 0.02 | 0.06 | 0.02 | 0.13 | 0.08 | 0.47 | 0.96 |
| 3rd quartile | 0.92 | 0.96 | 0.91 | 1.07 | 0.97 | 1.25 | 1.07 |
| Maximum | 9.38 | 7.62 | 9.38 | 5.91 | 9.38 | 4.11 | 1.32 |
| Correlation | 0.94 | 0.89 | 0.76 | 0.82 | 0.29 | ||
| n | 538 | 538 | 544 | 544 | 544 | 544 | 544 |
| Summary statistics for error distribution of point-estimation methods (gpc) | |||||
|---|---|---|---|---|---|
| Triangulation | Ordinary kriging | Polygonal declustering | Inverse distance squared | Local samle mean | |
| Mean | -0.00005 | 0.00631 | -0.03029 | -0.04323 | -0.04037 |
| Standard deviation | 0.507 | 0.679 | 1.008 | 0.923 | 1.408 |
| Minimum | -3.955 | -2.950 | -7.910 | -1.520 | -1.174 |
| 1st quartile | -0.005 | -0.138 | -0.063 | -0.398 | -0.938 |
| Median | 0.000 | -0.022 | 0.000 | -0.205 | -0.372 |
| 3rd quartile | 0.050 | 0.052 | 0.053 | -0.025 | 0.078 |
| Maximum | 2.365 | 6.601 | 4.730 | 7.489 | 8.308 |
| MAE | 0.233 | 0.303 | 0.463 | 0.512 | 0.916 |
| MSE | 0.256 | 0.460 | 1.015 | 0.853 | 1.979 |
| n | 538 | 544 | 544 | 544 | 544 |
Ordinary kriging is a weighted linear combination of the observed data. The weights are based on a model called the variogram. The variogram is the variance of the difference between two cups at the distance between the two cups. Through modeling, kriging attempts to minimize the prediction error variance to produce an unbiased estimate (Isaaks and Srivastava 1989). Because the findings showed that triangulation was the best prediction method, ordinary kriging was not used.
The Delaunay triangulation method that was used is a weighted linear combination. The result is that closer points receive more weight. Delaunay triangulation uses polygons to determine triangles. In figure 6, the known points are points 1, 2, and 3. The unknown point is V. Point 1 is weighted from area 1, which is the area of the largest triangle. This gives point 1 the most weight, because it is the closest point. Figure 7 illustrates the triangles generated from drop 201.
Triangulation was used to estimate gpc values between observed points. Plotting the estimated points with the observed points created the 10- by 5-foot grid in figure 8.
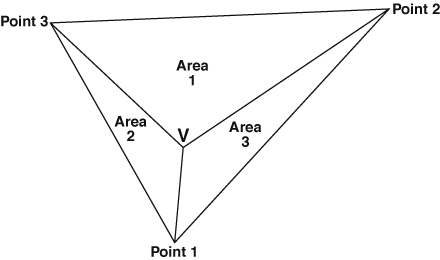
Figure 6—Three triangles constructed to estimate an unknown point.

Figure 7—Triangles constructed from sample points.
The contour plot generated by computer software was overlaid as in figure 8. Once the triangulation was complete, an algorithm was used to calculate line length.

Figure 8—Contour plot redrawn after triangulated gpc values were added to
observed gpc values.
Lengths of retardant line at different coverage levels are calculated by searching crossrange rows for values above a threshold. Line segments begin at the point of the first downrange value above the threshold and end at the point of the last value. The points immediately uprange and downrange of the starting and ending points are used to perform a linear interpolation between the two. This technique allows reporting lengths with accuracy greater than the grid spacing. Lengths for each coverage level of interest are reported as both longest continuous segment and total length. This provides an indication of overall continuity of the line. Uncertainty in coverage level is applied as a single estimated value to all points when checking for the threshold condition. A coverage level value of 3.98 will be at the threshold of 4.00 if the estimated uncertainty is 0.02.

